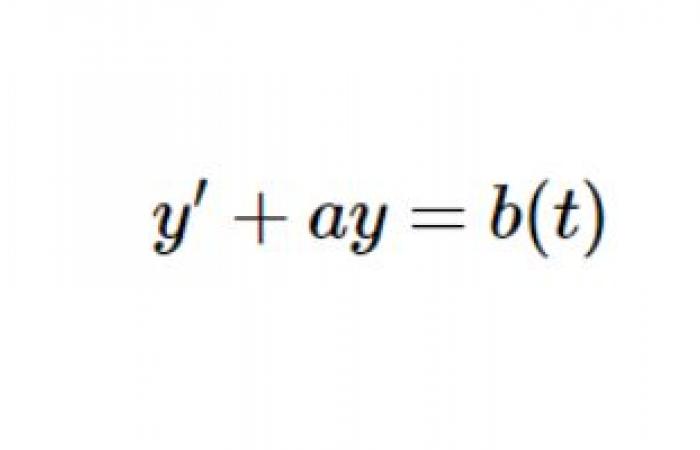Assenti dai programmi ECE/ECS, le equazioni differenziali stanno ritornando nel curriculum di matematica applicata. Questo concetto deve quindi essere padroneggiato a portata di mano.
Ma cos’è un’equazione differenziale?
Un’equazione differenziale è un’equazione che mette in relazione una funzione con le sue derivate. Questa funzione è l’incognita, che è generalmente indicata con ( y ), e dipende da una variabile, spesso indicata con ( t ) o ( x ).
Descrive come una quantità cambia in base a un’altra, come la velocità di un oggetto che dipende dal tempo. Queste equazioni vengono utilizzate per modellare vari fenomeni, come la crescita della popolazione, il movimento degli oggetti o i cambiamenti di temperatura.
Esistono diversi tipi di equazioni differenziali e, quindi, diversi metodi per risolverle.
Equazioni differenziali del primo ordine
Le equazioni differenziali del primo ordine sono equazioni della forma [ y’ + ay = b
dove ( b ) è una funzione continua su un intervallo ( I ) e ( t in I ).
L’equazione omogenea associato a ( (E) ) è ( y’ + ay = 0 (E_{0}) ).
Le soluzioni di ( (E_{0}) ) sono tutte funzioni ( g
Le soluzioni di ( (E)) sono la somma delle soluzioni di ( (E_{0}) ) e a particolare soluzione di ( (E)) .
Se (b) è una costante, lo è anche la soluzione particolare.
Se ( b ) non è una costante, la materia guida lo studente nella sua ricerca.
Equazioni differenziali del secondo ordine
Le equazioni differenziali del secondo ordine sono equazioni della forma ( y” + ay’ + by = c
dove ( c) è una funzione continua su un intervallo ( I ) e ( t in I ).
L’equazione omogenea associato a ( (E) ) è ( y” + ay’ + by = 0 (E_{0}) ).
L’equazione caratteristica di ( (E) ) è (r^{2} + ar + b = 0 (E_{c}) ).
Se ( (E_{c}) ) ammette un’unica soluzione su ( I ) indicato con ( r_{0} ), allora le soluzioni di ( (E) ) su ( I ) sono tutte le funzioni del modulo:
[ g
Se ( (E_{c}) ) ammette due soluzioni su ( I ) indicato con ( r_{1} ) e ( r_{2} ), allora le soluzioni di ( (E) ) su (I ) sono tutte funzioni della forma:
[ g
Le soluzioni di ( (E)) sono la somma delle soluzioni di ( (E_{0}) ) e a particolare soluzione di ( (E)) .
Se ( c ) è una costante, lo è anche la soluzione particolare.
Se ( c ) non è una costante, la materia guida lo studente nella sua ricerca.
La traiettoria
La traiettoria di un’equazione differenziale ( (E)) su( I ) è dell’insieme ({ (t, y
Possiamo ottenere una traiettoria unica imponendo condizioni iniziali del tipo ( y(t_{0}) = y_{0})
Se si tratta di un’equazione differenziale del primo ordine, sarà necessaria una condizione iniziale per ottenere una traiettoria unica.
Se si tratta di un’equazione differenziale del secondo ordine, saranno necessarie due condizioni iniziali per ottenere un’unica traiettoria.
Chiamiamo traiettoria di equilibrio qualsiasi traiettoria associata ad una soluzione costante.
Una traiettoria converge se ( y
Risolvere un sistema differenziale lineare a coefficienti costanti
Soit ( I in mathbb{R} ).
Chiamiamo sistema differenziale lineare omogeneo a coefficienti costanti un sistema della forma:
[
(S) begin{cases}
x’_1
dove ( t in I) e (x_1, dots, x_n ) sono n funzioni della variabile (t), differenziabili su (I), e (a_{11}, dots , a_{nn} ) sono (n^2) reali.
L’obiettivo della risoluzione di questo sistema è trovare le funzioni (x_1, dots, x_n).
Passaggio 1
Riscriviamo il sistema in forma matriciale:
In posa pour tout (t in I) :
[
X
Quindi, il sistema ((S)) può essere scritto come (X’
Attenzione : i passi successivi sono possibili solo se A è diagonalizzabile!
Passaggio 2
Diagonalizziamo (A) per scriverlo nella forma:
(A = PDP^{-1}), dove (D = begin{pmatrix} lambda_1 & 0 \ 0 & ddots & 0 \ 0 & 0 & lambda_n end{pmatrix} )
(D) è una matrice diagonale che contiene gli autovalori di (A) sulla sua diagonale.
(P) è una matrice invertibile composta dagli autovettori associati agli autovalori di (A), organizzati in colonne (attenzione a rispettare lo stesso ordine di D!)
Passaggio 3
Nella posa (Y
Otteniamo, per derivazione,[begin{align}
Y’
Su un alors : (Y’
), macchina (D=P^{-1}AP )
Sia (Y
)
(
Y’
)
(
Y’
)
(
Y’
)
(forall i in I, y_i
Su a quindi (Y
Passaggio 4
Troviamo (X
Passaggio 5 (se richiesto)
Risolviamo il sistema rispetto alle condizioni iniziali imposte.
Basta posizionare (t) nel nostro sistema ( X
: considerando il sistema ( (S) X’
Esempio
Risolvere i problemi del sistema:[
begin{cases}
x’
Passaggio 1
Passiamo alla scrittura della matrice. Otteniamo:[
X’
Passaggio 2
Diagonali A.
Non esitate a consultare questo articolo se non avete dimestichezza con i metodi per diagonalizzare una matrice.
Sia (lambda in mathbb{R}),
(
lambda text{ è un autovalore di A} Leftrightarrow A-lambda I = 0
)
(
A-lambda I = begin{pmatrice}
-lambda & 1 & 1 \
-1 & 2 – lambda & 1 \
1 & 0 & 1 – lambda end{pmatrix}
)
Utilizziamo il metodo pivot di Gauss
Facciamo (L_{1}leftrightarrow L_{3}):[
begin{pmatrix}
1 & 0 & 1-lambda \
-1 & 2-lambda & 1 \
-lambda & 1 & 1
end{pmatrix}
]
Quindi (L_{2}leftarrow L_{2}+L_{1}) e (L_{3}leftarrow L_{3}+lambda L_{1}) :[
begin{pmatrix}
1 & 0 & 1-lambda \
0 & 2-lambda & 2 -lambda \
0 & 1 & -lambda^{2} + lambda + 1
end{pmatrix}
]
Eseguiamo una disgiunzione dei casi
Per (2 – lambda ne 0), eseguiamo (L_{2}leftarrow frac{1}{(2 -lambda)L_{2}}):[
begin{pmatrix}
1 & 0 & 1-lambda \
0 & 1 & 1 \
0 & 1 & -lambda^{2} + lambda + 1
end{pmatrix}
]
Ciò semplifica i calcoli di (L_{3}leftarrow L_{3}- L_{2}):[
begin{pmatrix}
1 & 0 & 1-lambda \
0 & 1 & 1 \
0 & 0 & -lambda^{2} + lambda
end{pmatrix}
]
Nella posa ( A_{lambda} = begin{pmatrix}
1 & 0 & 1-lambda \
0 & 1 & 1 \
0 & 0 & -lambda^{2} + lambda
end{pmatrice})
begin{allineare}
lambda text{ è un autovalore di A} & Leftrightarrow -lambda^{2} + lambda = 0 \
& Leftrightarrow lambda (1 – lambda) = 0 \
& Leftrightarrowlambda = 0 text{o}lambda =
end{allineare}
Per (2 – lambda = 0), sia (lambda = 2)
Quindi (A – lambda I = A – 2I)[ A – 2I = begin{pmatrix}
1 & 0 & -2 \
0 & 0 & 0 \
0 & 1 & -1
end{pmatrix}
]
Osserviamo che la seconda colonna è zero, quindi il rango della matrice è minore o uguale a 2, quindi 2 è un autovalore di A.
Pertanto, gli autovalori di A sono ( fbox {(0, 1 text {e} 2)} ).
Calcoliamo quindi gli autospazi associati a 0, 1 e 2
Sia ( X = begin{pmatrice} x \ y \ zend{pmatrice}),
Per autovalore 0:
(
begin{allineare}
X in E_{0} & Leftrightarrow (A-0I)X = O \
& Leftrightarrow begin{cases} x + z = 0 \ y + z = 0 end{cases} \
& Leftrightarrow begin{cases} x = – z \ y = – z end{cases} \
& Leftrightarrow X in text{Vect}begin{pmatrix} 1 \ 1 \ – 1 end{pmatrix}
end{allineare}
)
Ainsi ( fbox {( E_{0} = text{Vect}begin{pmatrix} 1 \ 1 \ -1 end{pmatrix} )} )
Per autovalore 1:
(
A_{1} = begin{pmatrice}
1 & 0 & 0\
0 & 1 & 1 \
0 e 0 e 0
end{matrice}
)
(
begin{allineare}
X in E_{1} & Leftrightarrow A_{1}X = O \
& Leftrightarrow begin{cases} x = 0 \ y + z = 0 end{cases} \
& Leftrightarrow begin{cases} x = 0 frac{1}{2} x \ y = – z end{cases} \
& Leftrightarrow X in text{Vect}begin{pmatrix} 0 \ 1 \ – 1 end{pmatrix}
end{allineare}
)
Ainsi ( fbox {( E_{1} = text{Vect}begin{pmatrix} 0 \ 1 \ -1 end{pmatrix} )} )
Per autovalore 2:
(
A – 2I = begin{pmatrice}
-2 & 1 & 1 \
-1 & 0 & 1 \
1 e 0 e -1
end{matrice}
)
(
begin{allineare}
X in E_{2} & Leftrightarrow (A-2I)X = O \
& Leftrightarrow begin{cases} -2x + y + z = 0 \ -x + z = 0 \ x – z = 0 end{cases} \
& Leftrightarrow begin{cases} 2x + y + x = 0 \ x = z end{cases} \
& Leftrightarrow begin{cases} -x + y = 0 \ x = z end{cases} \
& Leftrightarrow begin{cases} y = x \ x = z end{cases} \
& Leftrightarrow X in text{Vect}begin{pmatrix} 1 \ 1 \ 1 end{pmatrix}
end{allineare}
)
Ainsi ( fbox {(E_{2} = text{Vect}begin{pmatrix} 1 \ 1 \ 1 end{pmatrix} )} )
A è di ordine 3 e ha tre autovalori, quindi ( fbox {( text{A è diagonalizzabile } )} ).
Possiamo quindi scrivere (A) nella forma (A=PDP^{-1})
con (
D = begin{pmatrice}
0 & 0 & 0 \
0 & 1 & 0 \
0 e 0 e 2
end{matrice}
)
E ( P = begin{pmatrice}
1 & 0 & 1 \
1 & 1 & 1 \
-1 e -1 e 1
end{pmatrice})
Calcoliamo ( P^{-1}) utilizzando il metodo pivot gaussiano. Se non sai come invertire una matrice, puoi consultare questo articolo.[
left[ begin{array}{ccc|ccc}
1 & 0 & 1 & 1 & 0 & 0 \
1 & 1 & 1 & 0 & 1 & 0 \
-1 & -1 & 1 & 0 & 0 & 1
end{array} right]
Su un:
]
Facciamo: ( L_{2} leftarrow L_{2}+L_{1}):[
left[ begin{array}{ccc|ccc}
1 & 0 & 1 & 1 & 0 & 0 \
0 & 1 & 0 & -1 & 1 & 0 \
-1 & -1 & 1 & 0 & 0 & 1
end{array} right]
]
Quindi ( L_{3} leftarrow L_{3}+L_{1}):[
left[ begin{array}{ccc|ccc}
1 & 0 & 1 & 1 & 0 & 0 \
0 & 1 & 0 & -1 & 1 & 0 \
0 & -1 & 2 & 1 & 0 & 1
end{array} right]
]
E ( L_{3} leftarrow L_{3}+L_{2}):[
left[ begin{array}{ccc|ccc}
1 & 0 & 1 & 1 & 0 & 0 \
0 & 1 & 0 & -1 & 1 & 0 \
0 & 0 & 2 & 0 & 1 & 1
end{array} right]
]
Quindi ( L_{3} leftarrow frac{1}{2}L_{3}):[
left[ begin{array}{ccc|ccc}
1 & 0 & 1 & 1 & 0 & 0 \
0 & 1 & 0 & -1 & 1 & 0 \
0 & 0 & 1 & 0 & frac{1}{2} & frac{1}{2}
end{array} right]
]
E ( L_{1} leftarrow L_{1}-L_{3}):[
left[ begin{array}{ccc|ccc}
1 & 0 & 0 & 1 & -frac{1}{2} & -frac{1}{2} \
0 & 1 & 0 & -1 & 1 & 0 \
0 & 0 & 1 & 0 & frac{1}{2} & frac{1}{2}
end{array} right]
]
Ainsi ( fbox {( P^{-1} = begin{pmatrix}
1 & -frac{1}{2} & -frac{1}{2} \
-1 & 1 & 0 \
0 & frac{1}{2} & frac{1}{2}
end{matrice} ) } )
Passaggio 3
Sia (Y
Otteniamo, per derivazione,
Su un alors : (Y’
), macchina (D=P^{-1}AP )
Sia (Y
X’
Y’
end{casi}
)
Soit ( (C_{1}, C_{2}, C_{3}) in mathbb{R}^{3} )
(
Y’
end{casi}
)
Su un donc (Y
C_{3}e^{2t}
end{pmatrice})
Passaggio 4
Troviamo (X
X
end{matrice}[ fbox {( begin{cases}
C_{1} + C_{3}e^{2t}\
C_{1} + C_{2}e^{t} + C_{3}e^{2t} \
– C_{1} – C_{2}e^{t} + C_{3}e^{2t}
end{cases} )}
]
)
Quindi la soluzione del sistema iniziale è
Non esitare a ripetere questo esercizio ancora e ancora finché non avrai compreso e memorizzato i diversi passaggi per risolvere un sistema di equazioni differenziali.
Potrai poi approfondire questo concetto grazie a questi articoli:
Puoi anche approfondire la tua maestria mettendoti alla prova con questi articoli:
Puoi trovare qui la mega-directory che contiene tutti i record del concorso e le risposte. Puoi anche accedere a tutte le nostre altre risorse matematiche qui!
-