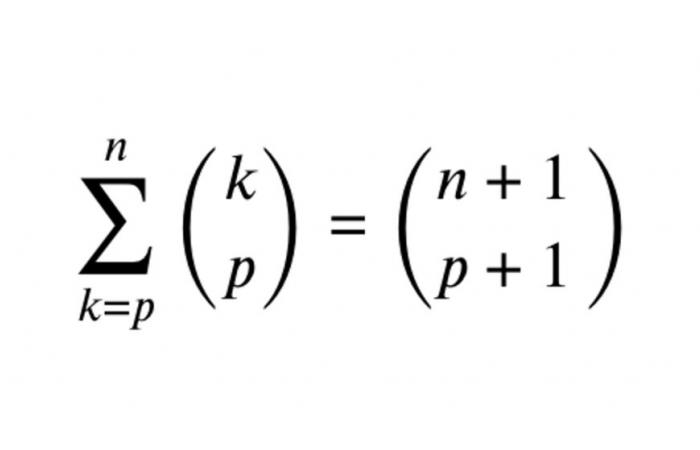La formula di iterazione di Pascal è un (molto) grande classico delle competizioni ECG, sia per i soggetti EDHEC/EM Lione ma anche per i soggetti parigini. Sebbene rimanga un concetto ai margini del programma, è molto veloce e relativamente facile da padroneggiare. Questo articolo ti invita ad analizzare questa formula di iterazione Pascal per assicurarti punti nel tuo futuro DS, CB o anche nella competizione!
Formula di iterazione di Pascal
Definizione
Soient (n, p in mathbb{N}) tels que (n geq p), (displaystyle sum_{k=p}^{n} {{k} choose {p} } = {{n+1} scegli {p+1}}).
Osservazioni:
- Usando il completamento del triangolo di Pascal a termini zero, possiamo anche scriverlo: (displaystyle sum_{k=0}^{n} {{k} choose {p}} = {{n+1} choose {p+1}}) con (n, p geq 0 ).
- Come promemoria, sappiamo che (displaystyle {{n} choose {k}} = 0) quando (k > n).
- Utilizzando la simmetria dei coefficienti binomiali, otteniamo la somma di una diagonale discendente, (displaystyle sum_{k=p}^{n} {{k} choose {kp}} = {{n+1} choose {p+1}}) per (n geq p ).
- Come promemoria, sappiamo che (displaystyle {{n} choose {k}} = {{n} choose {nk}}) con (n, k in mathbb{N}) e (n geq k).
Spiegazioni
La formula di iterazione di Pascal, chiamata anche formula del grondaia (o formula del bastone da hockey), dà il risultato di una somma finita di termini consecutivi di una colonna del triangolo di Pascal, a partire dal primo termine diverso da zero, come coefficiente binomiale situato a a destra e sotto l’ultimo termine.
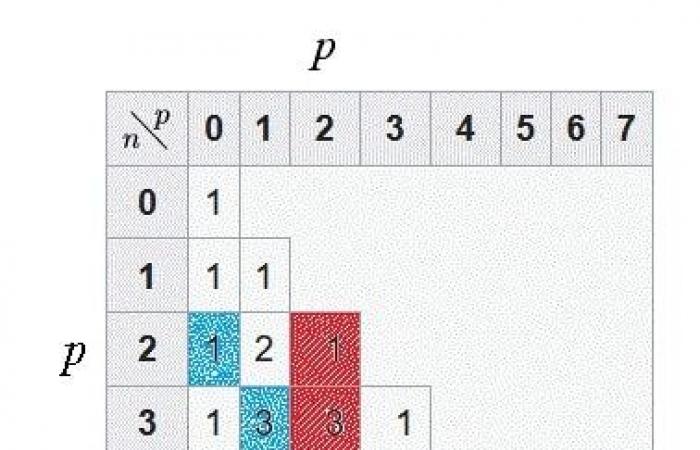
Spiegazione grafica con il triangolo di Pascal
Le caselle rosse sono quelle usate dalla formula per (n)=5, (p)=2; in blu, caso di diagonale discendente per gli stessi valori.
Nota: grazie a questo triangolo di Pascal, comprendiamo la logica dietro il titolo “formula del bastone da hockey”. Infatti le caselle rosse, che sono elementi della somma, e la casella rossa 20, che rappresenta il risultato della somma, formano una sorta di croce.
Dimostrazioni della formula di iterazione di Pascal
Le seguenti prime dimostrazioni si basano su un’altra proprietà di Pascal presente nel programma: (displaystyle {{n} choose {k}} = {{n-1} choose {k-1}} + {{n – 1} scegli {k}}). La chiamiamo “relazione di Pascal”. Graficamente, vediamo nella tabella sopra che la somma di due numeri consecutivi sulla stessa riga è uguale al numero che si trova sotto il secondo numero aggiunto.
Dimostrazione telescopica
begin{align*} displaystyle sum_{k=p}^{n} {{k} choose {p}} &= sum_{k=p}^{n} left( {{k+1 } choose {p+1}} – {{k} choose {p+1}} right) text{ dopo la relazione di Pascal} \ &= displaystyle {{p+1} choose {n+1}} – {{p+1} choose {p}} text{ par télescopage} \ &= displaystyle {{p+1} choose {n+1}}. end{allineare*}
Nota: questa dimostrazione della formula di iterazione di Pascal è la più breve, la più semplice e la più elegante delle tre. Lo consiglio vivamente!
Dimostrazione per induzione
Montroni che (displaystyle sum_{k=p}^{n} {{k} choose {p}} = {{n+1} choose {p+1}}) con (n, p in mathbb{N}) et (n geq p).
Inizializzazione : per (n)=(p), otteniamo 1=1
Eredità : Sia un certo ( n ) appartenente a ([![p, +infty[![).
On a : begin{align*} displaystyle sum_{k=p}^{n} {{k} choose {p}} &= {{n+1} choose {p+1}} text{ par hypothèse de récurrence.} \ displaystyle sum_{k=p}^{n+1} {{k} choose {p}} &= sum_{k=p}^{n} {{k} choose {p}} + {{n+1} choose {p}} \ &= {{n+1} choose {p+1}} + {{n+1} choose {p}} \ &= {{n+2} choose {p+1}}. end{align*}
Conclusion : la proposition est initialisée et héréditaire, donc par principe de récurrence, on a démontré la formule d’itération de Pascal.
Remarque : cette démonstration (comme la première) est rigoureuse. Cependant, comme toute récurrence, elle nécessite de connaître au préalable le résultat à démontrer. Ici, la formule d’itération de Pascal. Cela ne devrait pas poser trop de problèmes : la formule étant hors programme, il est quasiment certain que dans des sujets, on te demande « Montrer que… ».
Démonstration par itération de la relation de Pascal
begin{align*} text{On a } displaystyle {{n+1} choose {p+1}} &= {{n} choose {p}} + {{n} choose {p+1}} text{ d’après la relation de Pascal.} \ & = displaystyle {{n} choose {p}} + {{n-1} choose {p}} + {{n-1} choose {p+1}} \ & = displaystyle {{n} choose {p}} + {{n-1} choose {p}} + dots + {{n-k} choose {p}} + {{n-k} choose {p+1}} end{align*}
On pose (k)= (n) – (p) :
On a (displaystyle {{n+1} choose {p+1}} = {{n} choose {p}} + {{n-1} choose {p}} + cdots + {{p} choose {p}} + {{p} choose {p+1}}) ce qui donne bien la formule voulue.
Remarque : cette démonstration peut être utile à comprendre. Cependant, je ne conseille pas de l’apprendre et de l’utiliser, car les « … » sont souvent mal vus par des correcteurs très rigoureux. Privilégie la démonstration 1 ou 2.
Remarque générale : on peut également trouver des démonstrations de la formule d’itération de Pascal qui reposent sur la formule des séries géométriques ou encore sur le dénombrement, mais mieux vaut tout de même privilégier les démonstrations n° 1 et n° 2, bien plus classiques et plus connues des correcteurs. De plus, elles ne sont pas évidentes à comprendre et pourraient causer des erreurs d’étourderie.
Utilisation de la formule d’itération de Pascal
Exemples pratiques
La formule d’itération de Pascal est particulièrement utile pour retrouver les formules des sommes des premières puissances.
Si on développe notre formule, on obtient : [ displaystyle sum_{k=p}^{n} {k(k-1)cdots(k-p+1)} = frac{(n+1)(n)cdots(n-p+1)}{(p+1)}. ]
Per (p)=1, otteniamo la somma dei primi n interi naturali: [ displaystyle sum_{k=1}^{n} k = frac{n(n+1)}{2}. ]
Per (p)=2, troviamo [ displaystyle sum_{k=2}^{n} k(k-1) = frac{n(n-1)(n+1)}{3}, ] che ci permette di ottenere successivamente la somma dei primi n quadrati che vale [ displaystyle sum_{k=1}^{n} k^2 = frac{n(n+1)(2n+1)}{6}. ]
E per (p)=3, (p)=4…
Una cosa è certa, se in una materia ti viene chiesto di dimostrare la formula di iterazione di Pascal, è che dovrai utilizzarla nelle domande successive. Quindi restate sintonizzati!
Applicazioni del mondo reale
La formula di iterazione di Pascal viene applicata in vari campi per semplificare i calcoli combinatori e ottimizzare gli algoritmi:
- Nell’analisi combinatoria, per determinare la somma dei coefficienti binomiali e facilitare il conteggio dei sottoinsiemi.
- In informatica, per ottimizzare gli algoritmi e semplificare le espressioni della complessità.
- In probabilità e statistica, per calcolare le aspettative e le varianze delle variabili casuali combinatorie.
- Nella teoria dei grafi, per contare percorsi e cicli.
- In genetica, per analizzare combinazioni di tratti.
- In economia e ricerca operativa, per modellare e ottimizzare decisioni e sistemi.
Somma degli inversi dei termini di una colonna del triangolo di Pascal
Versare ( displaystyle n geq p geq 2 ),
[ displaystyle sum_{k=p}^{n} frac{1}{displaystyle {k choose p}} = frac{p}{p-1} left(1 – frac{1}{displaystyle {n choose p-1}}right) ]
COSÌ, [ displaystyle sum_{k=p}^{infty} frac{1}{displaystyle {k choose p}} = frac{p}{p-1} ] Arriviamo al risultato precedente perché [ displaystyle sum_{k=p}^{infty} frac{1}{displaystyle {k choose p}} = displaystyle sum_{k=p}^{n} frac{1}{displaystyle {k choose p}} + displaystyle sum_{k=n+1}^{infty} frac{1}{displaystyle {k choose p}} ]
e telescopicamente da [ displaystyle frac{1}{displaystyle {k choose p}} = frac{p}{p-1} left( frac{1}{displaystyle {k-1 choose p-1}} – frac{1}{displaystyle {k choose p-1}} right) ] che deriva dalla relazione: [ displaystyle (p-1) {k-1 choose p-1} {k choose p-1} = p {k-2 choose p-1} {k choose p} ]
Infine, possiamo scrivere la somma come segue: [ displaystyle sum_{k=p}^{infty} frac{1}{k(k-1)cdots (k-p+1)} = frac{1}{(p-1)!(p-1)} ]
Argomento che invoca la dimostrazione dell’iterazione di Pascal
Problema EDHEC 2016
Conclusione
Ora hai imparato la formula di iterazione di Pascal, sei in grado di dimostrare questa relazione e di comprenderne le varie applicazioni! Anche se questo concetto potrebbe non essere nel programma, comprenderlo ti sarà utile se incontri problemi combinatori complessi. Ci auguriamo che questo articolo di Major-prépa ti abbia fornito chiarimenti e abbia arricchito la tua comprensione degli strumenti combinatori.
Puoi trovare la mega-directory che contiene tutti i record del concorso e le risposte. Puoi anche accedere a tutte le nostre altre risorse matematiche!